Got a query asking How to Calculate the volume occupied by torispherical dish of a batch reactor,
this query will definitely have a solution, but usually many engineers will keep following some of the thumb rules those are applicable here, and some of the others will apply whatever thumb they remember, so its better to use thumb rule practically, but before that its very recommend to know the reason behind deriving the thumb.
So before going into calculation directly, first of all we should know some basic concepts involved in the design of torispherical dish [doom/disc].,
** Crown Radius: A torispherical dish is the surface obtained from the intersection of a spherical cap with a tangent torus, as Shown in above pic. The radius of the sphere R is called the "crown radius,"
** Knuckle Radius: The Radius of the circle's those are formed at the transition phase from spherical surface to flat surface is called Knuckle Radius, Usually the sphere's / circle's those were formed at those transition phases were called Torus, and in plural form mentioned as Torii, so having torii is the reason behind deriving the name as torispherical dishes, And
generally the knucle radius of a torispherical dish will be 0.6 times the diameter of the vessel.
Usually these torispherical dishes were designed for the sake of pressure vessels and storage vessels, to avoid the breathing losses in such vessels these dishes were designed.
** Critical Radius: The Radius where the transition occurs from Spherical to Torus is called as Critical Radius.,
So, if you are clear with the above basic definitions we can enter into calculation part,
Let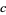 be the distance from the center of the torus to the center of the torus tube, let 'c' be the radius of the torus tube, and let 'h' be the height from the base of the dome to the top. Then the radius of the base is given by a + c < R. In addition, by elementary geometry, a torispherical dome satisfies
be the distance from the center of the torus to the center of the torus tube, let 'c' be the radius of the torus tube, and let 'h' be the height from the base of the dome to the top. Then the radius of the base is given by a + c < R. In addition, by elementary geometry, a torispherical dome satisfies
The transition from sphere to torus occurs at the critical radius
So from the basic Dome equation from 3d Co-ordinate geometry, we are having two equations based on different cases
So, these are the theoretical Myth that our thumb is basing , and now i'm gonna tell you the thumb for calculating the Torispherical end volume,
Volume occupied by torispherical dish, V= (Pi/24)* Di*Di*Di.,
And some people want to have some clarity even through Thumb, so for them practice this,
Volume, V= [0.0847*Di*Di*Di]+ [ (pi*Di*Di*S.F)/4].
Thats it......Cheers,
Comments are appreciated......!!!!!
Some of the Readers wont have much time to read and digest all the above theory and may need instant results, for them i have developed an excel sheet, use that sheet for calculation,
About The Author

this query will definitely have a solution, but usually many engineers will keep following some of the thumb rules those are applicable here, and some of the others will apply whatever thumb they remember, so its better to use thumb rule practically, but before that its very recommend to know the reason behind deriving the thumb.
So before going into calculation directly, first of all we should know some basic concepts involved in the design of torispherical dish [doom/disc].,
** Crown Radius: A torispherical dish is the surface obtained from the intersection of a spherical cap with a tangent torus, as Shown in above pic. The radius of the sphere R is called the "crown radius,"
** Knuckle Radius: The Radius of the circle's those are formed at the transition phase from spherical surface to flat surface is called Knuckle Radius, Usually the sphere's / circle's those were formed at those transition phases were called Torus, and in plural form mentioned as Torii, so having torii is the reason behind deriving the name as torispherical dishes, And
generally the knucle radius of a torispherical dish will be 0.6 times the diameter of the vessel.
Usually these torispherical dishes were designed for the sake of pressure vessels and storage vessels, to avoid the breathing losses in such vessels these dishes were designed.
You May Also Like:
** Critical Radius: The Radius where the transition occurs from Spherical to Torus is called as Critical Radius.,
So, if you are clear with the above basic definitions we can enter into calculation part,
Let
The transition from sphere to torus occurs at the critical radius
Volume occupied by torispherical dish, V= (Pi/24)* Di*Di*Di.,
And some people want to have some clarity even through Thumb, so for them practice this,
Volume, V= [0.0847*Di*Di*Di]+ [ (pi*Di*Di*S.F)/4].
Thats it......Cheers,
Comments are appreciated......!!!!!
Some of the Readers wont have much time to read and digest all the above theory and may need instant results, for them i have developed an excel sheet, use that sheet for calculation,
You May Also Like:
About The Author
Hi! I am Ajay Kumar Kalva, Currently serving as the CEO of this site, a tech geek by passion, and a chemical process engineer by profession, i'm interested in writing articles regarding technology, hacking and pharma technology.
Follow Me on Twitter AjaySpectator & Computer Innovations
Follow Me on Twitter AjaySpectator & Computer Innovations











 Hi! I am Ajay Kumar Kalva, owner of this site, a tech geek by passion, and a chemical process engineer by profession, i'm interested in writing articles regarding technology, hacking and pharma technology.
Hi! I am Ajay Kumar Kalva, owner of this site, a tech geek by passion, and a chemical process engineer by profession, i'm interested in writing articles regarding technology, hacking and pharma technology. 
Dear Ajay, here you given the volume occupied by the torispherical dish pi/24*di^3, is it only for one dish or two dishes? noramally reactor have two dishes. And what is the meaning of S.F below this eqation?
ReplyDeleteIt is the single dish tentative volume, S.F. means height of straight flange.
DeleteRegards,
AJAY K
Is this volume including SF length of dish ??? Please reply
ReplyDeleteyeah
Deletewhat is Di
ReplyDeleteInternal dia
DeleteDear sir
ReplyDeleteCan you please give a example with data
It would be glad to hear from you
Thanking you
Warm regards
Preetam yadav